Sometimes you want to produce maps with special layouts. I specially like maps with modified geometries, e.g. simplifiying the original shapes to squares or dots. When doing a little search over the web I found the fantastic post Fishnets and Honeycomb: Square vs. Hexagonal Spatial Grids by Matt Strimas-Mackey that was a huge inspiration (by the way, don’t miss his blog, full of very interesting pieces of work).
The only thing I was not completely comfortable with was that the post used the old-fashioned sp package instead of my personal fav, the sf package, (the post was published in 2016, note that author has also moved to the sf package since then). So I decided to explore further options with sf.
The approach is similar (using grids over a map and work with that) but using st_make_grid. I also expanded it by grouping the grids and also producing dots over the geometries. So basically I produced 5 variations of the map:
| Type | Replacement | Grouped |
|---|---|---|
| Fishnet | Square | No |
| Puzzle | Square | Yes |
| Honeycomb | Hexagon | No |
| Hexbin | Hexagon | Yes |
| Pixel | Dot | No |
Required R packages
library(sf)
library(giscoR)
library(dplyr)
library(RColorBrewer)
Working with square grids
Let’s use the square option of st_make_grid and play a bit with it.
GB <- ne_download(50,
type = "map_subunits",
returnclass = "sf",
destdir = tempdir()
) %>%
subset(CONTINENT == "Europe") %>%
subset(ADM0_A3 == "GBR")
# Projecting and cleaning
GB <- st_transform(GB, 3857) %>% select(NAME_EN, ADM0_A3)
initial <- GB
initial$index_target <- 1:nrow(initial)
target <- st_geometry(initial)
# Create my own color palette
mypal <- colorRampPalette(c("#F3F8F8", "#008080"))
Warning: The cellsize should be established in the same unit that the projection (in this case is meters). Pay special attention on this, given that if the parameter is too small (meaning that the grid is too dense) R could crash easily.
grid <- st_make_grid(target,
50 * 1000,
# Kms
crs = st_crs(initial),
what = "polygons",
square = TRUE
)
# To sf
grid <- st_sf(index = 1:length(lengths(grid)), grid) # Add index
# We identify the grids that belongs to a entity by assessing the centroid
cent_grid <- st_centroid(grid)
cent_merge <- st_join(cent_grid, initial["index_target"], left = F)
grid_new <- inner_join(grid, st_drop_geometry(cent_merge))
# Fishnet
Fishgeom <- aggregate(grid_new,
by = list(grid_new$index_target),
FUN = min,
do_union = FALSE
)
# Lets add the df
Fishnet <- left_join(
Fishgeom %>% select(index_target),
st_drop_geometry(initial)
) %>%
select(-index_target)
# Now lets create the Puzzle
Puzzlegeom <- aggregate(st_buffer(grid_new, 0.5), # Avoid slivers
by = list(grid_new$index_target),
FUN = min,
do_union = TRUE
) # This changes!!!
Puzzle <- left_join(
Puzzlegeom %>% select(index_target),
st_drop_geometry(initial)
) %>%
select(-index_target)
# Plot
par(mfrow = c(1, 2), mar = c(1, 1, 1, 1), bg = NA)
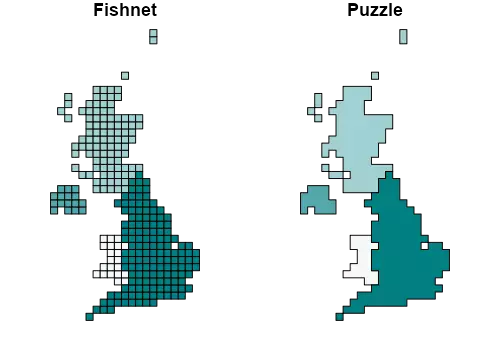
plot(st_geometry(Fishnet), col = mypal(4), main = "Fishnet")
plot(st_geometry(Puzzle), col = mypal(4), main = "Puzzle")
Going hex
Extremely easy. We just need to change the square parameter of st_make_grid from TRUE to FALSE
grid <- st_make_grid(target,
50 * 1000, # Kms
crs = st_crs(initial),
what = "polygons",
square = FALSE # This is the only piece that changes!!!
)
# Make sf
grid <- st_sf(index = 1:length(lengths(grid)), grid) # Add index
# We identify the grids that belongs to a entity by assessing the centroid
cent_grid <- st_centroid(grid)
cent_merge <- st_join(cent_grid, initial["index_target"], left = F)
grid_new <- inner_join(grid, st_drop_geometry(cent_merge))
# Honeycomb
Honeygeom <- aggregate(
grid_new,
by = list(grid_new$index_target),
FUN = min,
do_union = FALSE
)
# Lets add the df
Honeycomb <- left_join(
Honeygeom %>%
select(index_target),
st_drop_geometry(initial)
) %>%
select(-index_target)
# Now lets create the Hexbin
Hexbingeom <- aggregate(
st_buffer(grid_new, 0.5), # Avoid slivers
by = list(grid_new$index_target),
FUN = min,
do_union = TRUE
)
Hexbin <- left_join(
Hexbingeom %>%
select(index_target),
st_drop_geometry(initial)
) %>%
select(-index_target)
# Plot
par(mfrow = c(1, 2), mar = c(1, 1, 1, 1), bg = NA)
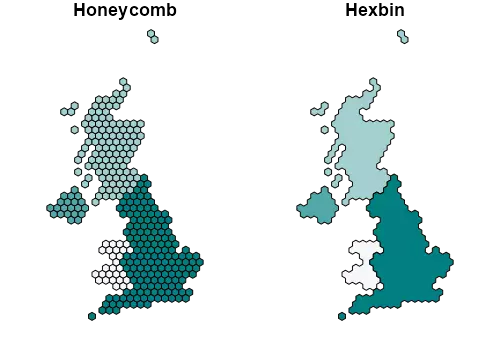
plot(st_geometry(Honeycomb), col = mypal(4), main = "Honeycomb")
plot(st_geometry(Hexbin), col = mypal(4), main = "Hexbin")
Pixel it!
Also quite easy, just a couple of tweaks more, always using st_make_grid.
grid <- st_make_grid(target,
50 * 1000, # Kms
crs = st_crs(initial),
what = "centers"
)
# Make sf
grid <- st_sf(index = 1:length(lengths(grid)), grid) # Add index
# We identify the grids that belongs to a entity by assessing the centroid
cent_grid <- st_centroid(grid)
cent_merge <- st_join(cent_grid, initial["index_target"], left = F)
grid_new <- st_buffer(cent_merge, 50 * 1000 / 2)
Pixelgeom <- aggregate(
grid_new,
by = list(grid_new$index_target),
FUN = min,
do_union = FALSE
)
# Lets add the df
Pixel <- left_join(
Pixelgeom %>%
select(index_target),
st_drop_geometry(initial)
) %>%
select(-index_target)
# Plot
par(mfrow = c(1, 1), mar = c(1, 1, 1, 1), bg = NA)
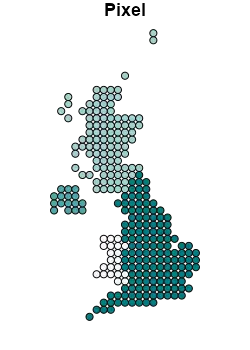
plot(st_geometry(Pixel), col = mypal(4), main = "Pixel")
Wrap up
So finally I wrapped all that in a function (see the code in my repo), that I named stdh_gridpol:
stdh_gridpol <- function(sf,
to = "fishnet",
gridsize = as.integer(
min(
diff(st_bbox(sf)[c(1, 3)]),
diff(st_bbox(sf)[c(2, 4)])
) / 40
),
sliver = 0.5) {
if (!unique(st_geometry_type(sf)) %in% c("POLYGON", "MULTIPOLYGON")) {
stop("Input should be MULTIPOLYGON or POLYGON")
}
if (!to %in% c("fishnet", "puzzle", "honeycomb", "hexbin", "pixel")) {
stop("'to' should be 'fishnet','puzzle','honeycomb','hexbin' or 'pixel'")
}
if (class(sf)[1] == "sf") {
initial <- sf
initial$index_target <- 1:nrow(initial)
} else {
initial <- st_sf(index_target = 1:length(sf), geom = sf)
}
target <- st_geometry(initial)
if (to %in% c("fishnet", "puzzle")) {
sq <- T
} else {
sq <- F
}
if (to == "pixel") {
grid <- st_make_grid(target,
gridsize,
crs = st_crs(initial),
what = "centers"
)
} else {
grid <- st_make_grid(
target,
gridsize,
crs = st_crs(initial),
what = "polygons",
square = sq
)
}
grid <- st_sf(index = 1:length(lengths(grid)), grid) # Add index
if (to == "pixel") {
cent_merge <- st_join(grid, initial["index_target"], left = F)
grid_new <- st_buffer(cent_merge, gridsize / 2)
} else {
cent_grid <- st_centroid(grid)
cent_merge <- st_join(cent_grid, initial["index_target"], left = F)
grid_new <- inner_join(grid, st_drop_geometry(cent_merge))
}
if (to %in% c("fishnet", "honeycomb", "pixel")) {
geom <- aggregate(
grid_new,
by = list(grid_new$index_target),
FUN = min,
do_union = FALSE
)
} else {
geom <- aggregate(
st_buffer(grid_new, sliver),
by = list(grid_new$index_target),
FUN = min,
do_union = TRUE
)
}
if (class(initial)[1] == "sf") {
fin <- left_join(
geom %>% select(index_target),
st_drop_geometry(initial)
) %>%
select(-index_target)
fin <- st_cast(fin, "MULTIPOLYGON")
return(fin)
} else {
fin <- st_cast(geom, "MULTIPOLYGON")
return(st_geometry(fin))
}
}
# End of the function-----
fish <- stdh_gridpol(GB, to = "fishnet", gridsize = 50 * 1000)
puzz <- stdh_gridpol(GB, to = "puzzle", gridsize = 50 * 1000)
hon <- stdh_gridpol(GB, to = "honeycomb", gridsize = 50 * 1000)
hex <- stdh_gridpol(GB, to = "hexbin", gridsize = 50 * 1000)
pix <- stdh_gridpol(GB, to = "pixel", gridsize = 50 * 1000)
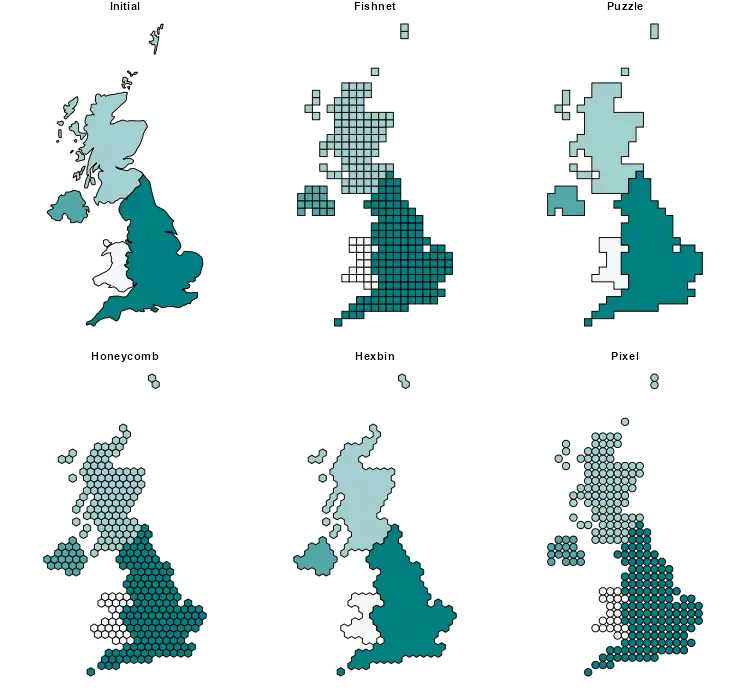
And that’s it! The function stdh_gridpol has some alert mechanisms, as accepting only POLYGON or MULTIPOLYGON, and the default value of gridsize is computed in a way that the shortest dimension would have 40 cells.